Monday May 13, 2024

home | contact | Support | Fractals Natures pattern... | Fractals Natures pattern...

Fractals

Natures pattern...

Fractals > Fractal Algorithms in 2-Dimensions

Well-known and widely appreciated 2D fractal algorithms

• Mandelbrot Set: The classic fractal that remains one of the most well-known and studied. It's generated by iterating a simple mathematical formula.
• Julia Set: Similar to the Mandelbrot set but allows for variation by using a complex parameter. Julia sets can exhibit a wide range of intricate patterns.
• Sierpinski Triangle: A classic fractal generated by recursively removing triangles from a larger triangle, creating a self-replicating pattern.
• Koch Snowflake: A self-replicating fractal curve with increasing levels of complexity, generated by adding triangles to each segment of an equilateral triangle.
• Dragon Curve: A self-replicating curve derived from an iterative process that alternates between two directions, resulting in a visually interesting pattern.
• Barnsley Fern: An iterated function system (IFS) fractal that simulates the growth of a fern by applying affine transformations.
• Apollonian Gasket: A fractal pattern formed by recursively adding circles within circles and removing the intersecting regions.
• Menger Sponge: A 2D representation of the Menger sponge, created by recursively removing squares from a larger square to form a self-replicating pattern.
• Cantor Set: A simple yet elegant fractal generated by removing the middle portion of an interval repeatedly, resulting in a set with zero length.
• Pythagorean Tree: A fractal generated by recursively adding branches to a tree structure based on the Pythagorean theorem, creating a visually appealing geometric pattern.
• Tetrahex Fractal (Flat 2D Version): The Tetrahex Fractal is a geometric fractal created by recursively subdividing equilateral triangles into smaller equilateral triangles
• Burning Ship: Burning ship fractal is a variant on the mandelbrot set.
• Kaleidoscope Fractal: Kaleidoscope fractal is a type of fractal pattern that exhibits symmetrical and repetitive structures resembling those seen in a kaleidoscope.
There are a diverse range of fractal algorithms from geometric patterns to complex mathematical sets. The beauty of fractals lies in their ability to produce intricate and visually striking structures with relatively simple mathematical rules.

The following provides a set of self-contained implementations written in Javascript. Each of the examples provides working code and a screenshot to see the expected output. There are also a set of 'try yourself' tasks to help you explore and understand the fractal further (rather than just looking and trying to remember the code but making it stand up and dance for you).

Mandelbrot Set in Javascript

Click for details

In less than 100 lines of Javascript (in fact, include the HTML, CSS and JS, it's still less than 100 lines). Probably about 50 lines ;)

The following is a complete Javascript program you can run to see a Mandelbrot Set fractal.

<html>
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>xbdev.net - Mandelbrot Set Fractal Example</title>
  <style>
    body {
      margin  : 0;
      display : flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas { border: 1px solid #fff; }
  </style>
</head>
<body>
  <canvas id="mandelbrotCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('mandelbrotCanvas');
    const ctx    = canvas.getContext('2d');
    const width  = canvas.width;
    const height = canvas.height;

const maxIterations = 100;

function mandelbrot(c) {
      let z = { real: 0, imaginary: 0 };
      let n = 0;

while (z.real * z.real + z.imaginary * z.imaginary <= 4 && n < maxIterations) {

const nextZReal      = z.real * z.real - z.imaginary * z.imaginary + c.real;
        const nextZImaginary = 2 * z.real * z.imaginary + c.imaginary;

z.real      = nextZReal;
        z.imaginary = nextZImaginary;

n++;
      }

if (n === maxIterations) { return 0; }
      return n / maxIterations;
    }

function drawMandelbrot() {
      for (let x = 0; x < width; x++) {
        for (let y = 0; y < height; y++) {
          const cx = (x - width / 2) * 4 / width;
          const cy = (y - height / 2) * 4 / height;
          const color = mandelbrot({ real: cx, imaginary: cy });

ctx.fillStyle = `hsl(0, 100%, ${color * 100}%)`;
          ctx.fillRect(x, y, 1, 1);
        }
      }
    }

drawMandelbrot();
  </script>
</body>
</html>

Example output would look something like:

Things To Try

Looking at the Mandelbrot code, it's not that scary! It shouldn't be - it's less than 100 lines (everythign). You can spend some time, researching and breaking down what's happening - essentially, it's iterating over a canvas and using the Mandelbrot set to determine what color to set the pixel output.

These tasks are fun ideas to take your mastery of fractals and the Mandelbrot set to the next level - also a chance to create even more fun and stunning visuals.

• Modify Mandelbrot code so more colors are used (e.g., inside/outside of the shape are different colors). Then do gradient colors (for the z-value - e.g., blue to green to red).
• Try animating the threashold (default is 4) - but try modifying it (e.g., 3.9 to 4.1). Also create an animation effect (as the threashold changes it updates in realtime to the viewer can see how it changes)
• Multiple Mandelbrot sets (run the algorithm multiple times and add the patterns) - initially you could do it by adding the colors in the final output (black - 0 and white - 1 so black won't add anything to the output).
• Shift the Mandelbrot result (add an offset so the mandelset is drawn at different locations on the screen)
• Draw 2 Mandelbrot set algorithms, each having a different offset, and create a final result (combine the z from both - not just a single one)
• Take the 2 Mandelbrot set example and animate it

Advanced Tasks
These might take a bit more work - depending on your understanding of things.
• Try modifying the equation so it's non-linear (e.g., scaling/shifting/offseting the complex number value during each iteration)
• Adding noise into the iteration loop (add or scale by a small random amount and see how it impacts the final fractal)
• If you're interested in optimization and parallel architectures like the GPU - you could try porting the implementation to WebGL or WebGPU API/Shader (run in real-time)
• Add an save button so you can save the generated fractal to a png or jpg (e.g., convert the canvas to image)
• 3D 'vector' version - instead of storing 'pixels' - try and store the points - then 'extrude' them (tessilate the surface)
• The example draws on a 2D plane - try and draw a 3D version - by 'rotating' around an axis (you'll probably need to look into ray-tracing or voxels)

Julia Set Fractal

Click for details

<html>
<head>
    <title>xbdev.net Julia Set Fractal (2d)</title>
    <style>
        body {
            margin: 0;
            overflow: hidden;
        }
        canvas {
            display: block;
        }
    </style>
</head>
<body>
    <canvas id="canvas"></canvas>
    <script>
        // Define canvas and context
        const canvas = document.getElementById('canvas');
        const ctx = canvas.getContext('2d');

// Set canvas size
        const width = canvas.width = window.innerWidth;
        const height = canvas.height = window.innerHeight;

// Define constants for the fractal
        const maxIterations = 100;
        const zoom = 200;
        const offsetX = 2;
        const offsetY = 1.5;
        const escapeRadius = 2;
        const cRe = -0.7;
        const cIm = 0.27015;

// Function to calculate Julia Set fractal
        function julia(x0, y0) {
            let x = x0;
            let y = y0;
            let i = 0;

while (x * x + y * y < escapeRadius * escapeRadius && i < maxIterations) {
                const xTemp = x * x - y * y + cRe;
                y = 2 * x * y + cIm;
                x = xTemp;
                i++;
            }

if (i === maxIterations) {
                return 0;
            } else {
                return i / maxIterations * 255;
            }
        }

// Render the fractal
        function render() {
            for (let x = 0; x < width; x++) {
                for (let y = 0; y < height; y++) {
                    const zx = (x / zoom) - offsetX;
                    const zy = (y / zoom) - offsetY;
                    const color = julia(zx, zy);
                    ctx.fillStyle = `rgb(${color}, ${color}, ${color})`;
                    ctx.fillRect(x, y, 1, 1);
                }
            }
        }

// Render the fractal when the page loads
        window.onload = function() {
            render();
        };
    </script>
</body>
</html>

Output should look something like this:

Things to Try

• Add colors (instead of black and white - gradient of colors showing the different information)
• Randomness - add smoe randomness to make the patterns/shape more creative
• Draw the fractal at different locations (x,y offset) also scale and rotation
• Draw multiple fractals on the screen at different locations with different parameters
• Instead of 'pixels' try and store the fractal as vector points and then draw the vector points

Sierpinski Triangle Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>xbdev.net Sierpinski Triangle Fractal Example</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="sierpinskiCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('sierpinskiCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawSierpinski(x, y, size, depth) {
      if (depth === 0) {
        // Draw a triangle
        ctx.beginPath();
        ctx.moveTo(x, y);
        ctx.lineTo(x + size, y);
        ctx.lineTo(x + size / 2, y + size * Math.sqrt(3) / 2);
        ctx.closePath();
        ctx.fillStyle = 'white';
        ctx.fill();
      } else {
        // Recursive calls for three smaller triangles
        const newSize = size / 2;

drawSierpinski(x, y, newSize, depth - 1);
        drawSierpinski(x + newSize, y, newSize, depth - 1);
        drawSierpinski(x + newSize / 2, y + newSize * Math.sqrt(3) / 2, newSize, depth - 1);
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const initialSize = 600;
      const initialDepth = 5;
      const initialX = (width - initialSize) / 2;
      const initialY = (height - initialSize * Math.sqrt(3) / 2) / 2;

drawSierpinski(initialX, initialY, initialSize, initialDepth);
    }

drawFractal();
  </script>
</body>
</html>

Output should look something like this:

Things to Try

Fun things to try with the Sierpinski triangle code.
• Colors - try making the different levels a different color (e.g., recursive depth change the color)
• Animating the effect (e.g., triangles can be added to a list and they interpolate 'grow') - don't just throw them on screen but try and create a slowly changing effect
• Rotate the triangle (static first then animated it rotating)
• User input - press the cursor keys (up/down) to add/remove the number of recurssions and the size/detail of the shape
• Multiple Sierpinksi triangles (add a second triangle and combine the visual effect) - do this at the pixel level and at the algorithm level
• Randomness - add some randomness to the algorithm (e.g., offsets, sizes, ...)

Koch Snowflake Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>xbdev.net Koch Snowflake Fractal Examples</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="kochCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('kochCanvas');
    const ctx    = canvas.getContext('2d');
    const width  = canvas.width;
    const height = canvas.height;

function drawKoch(x1, y1, x2, y2, depth) {
      if (depth === 0) {
        ctx.beginPath();
        ctx.moveTo(x1, y1);
        ctx.lineTo(x2, y2);
        ctx.strokeStyle = 'white';
        ctx.stroke();
      } else {
        const deltaX = x2 - x1;
        const deltaY = y2 - y1;

const x3 = x1 + deltaX / 3;
        const y3 = y1 + deltaY / 3;

const x4 = x1 + (deltaX / 3) + (Math.sqrt(3) / 6) * deltaY;
        const y4 = y1 + (deltaY / 3) - (Math.sqrt(3) / 6) * deltaX;

const x5 = x1 + (2 * deltaX / 3);
        const y5 = y1 + (2 * deltaY / 3);

drawKoch(x1, y1, x3, y3, depth - 1);
        drawKoch(x3, y3, x4, y4, depth - 1);
        drawKoch(x4, y4, x5, y5, depth - 1);
        drawKoch(x5, y5, x2, y2, depth - 1);
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const depth = 4;
      const size = 500;
      const x1 = (width - size) / 2;
      const y1 = (height - (Math.sqrt(3) / 2) * size) / 2;
      const x2 = x1 + size;
      const y2 = y1;
      const x3 = x1 + size / 2;
      const y3 = y1 + (Math.sqrt(3) / 2) * size;

drawKoch(x1, y1, x2, y2, depth);
      drawKoch(x2, y2, x3, y3, depth);
      drawKoch(x3, y3, x1, y1, depth);
    }

drawFractal();
  </script>
</body>
</html>

Output should look something like this:

Things to Try

Few things to try once you've got your snowflake on screen - add a bit of pizazz!

• Color - inside and outside are two unique colors (e.g., blue/red)
• Different levels of detail (depth/recursive function) - different levels add differenet/colors/gradients
• Animate the effect (as more detail is added it intepolates and gradually shows the changes - not just 'pops')
• Randomness - insert some small random values
• Draw multiple snowflakes on screen (each offset and located at a different point - also rotated and scaled - each unique)
• Instead of drawing to a pixel - store the surface points as vectors in an array - then extrude and create a 3D shape/visualization (required using WebGL/WebGPU)
• Modifying the base algorithm/calculation (e.g., sine wave, multiple/scale/addition - to warp/modify the snowflake for artistic effect)

Dragon Curve Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>xbdev.net Dragon Curve Fractal Example</title>
  <style>
    body {
      min-height: 700px;
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="dragonCurveCanvas" width="800" height="600"></canvas>
  <script>
    const canvas = document.getElementById('dragonCurveCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawDragonCurve(order, length, direction, startX, startY) {
      if (order === 0) {
        const endX = startX + length * Math.cos(direction);
        const endY = startY + length * Math.sin(direction);
        ctx.lineTo(endX, endY);
      } else {
        const newLength = length / Math.sqrt(2);

drawDragonCurve(order - 1, newLength, direction + Math.PI / 4, startX, startY);
        drawDragonCurve(order - 1, newLength, direction - Math.PI / 4, startX + newLength * Math.cos(direction + Math.PI / 4), startY + newLength * Math.sin(direction + Math.PI / 4));
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      ctx.beginPath();
      const order = 10;
      const length = 300;
      const startX = width/2;
      const startY = height / 4;
      const direction = Math.PI / 2;

ctx.moveTo(startX, startY);
      drawDragonCurve(order, length, direction, startX, startY);
      ctx.strokeStyle = 'white';
      ctx.stroke();
    }

drawFractal();
  </script>
</body>
</html>

Output should look like this:

Things to Try

• Color is the first things - instead of a basic 'white' - add in some variety showing different information, such as, recurrsion depth or distance from the centre (use gradients - red, blue to green)
• Animate the fractal rotating
• Add 'User Input' - increase/decreases orders dyanimcally by pressing up or down cursor keys
• Plot the 'order' vs time it takes to render (e.g., default is 10 - but higher values, like 30 will take a long long time to draw)
• Try different stroke patterns
• Draw multiple Dragon Curves and add them
• Box - 4 Dragon Curves (left, right, top, bottom with the middle empty - rotate and position them around the edge)
• Explore 'splines' to make the curves/edges more rounded (also try combining this with a lower order - to create the illusion of a smoother complex fractal with rounded edges - asthetics)
• Randomness - try adding in small amounts of random values to the calculation (make the final result have slight anomalies - visual effect)
• Magnifiying and changing the algorithm calculation - mix in some other trignometric functions, scale/offset by non-linear values to explore the visual result
• Try implementing the result in WebGL or WebGPU (shaders)

Barnsley Fern Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>xbdev.net Barnsley Fern Fractal Example</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="barnsleyFernCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('barnsleyFernCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawBarnsleyFern(iterations) {
      let x = 0;
      let y = 0;

for (let i = 0; i < iterations; i++) {
        const random = Math.random();
        let newX, newY;

if (random < 0.01) {
          newX = 0;
          newY = 0.16 * y;
        } else if (random < 0.86) {
          newX = 0.85 * x + 0.04 * y;
          newY = -0.04 * x + 0.85 * y + 1.6;
        } else if (random < 0.93) {
          newX = 0.2 * x - 0.26 * y;
          newY = 0.23 * x + 0.22 * y + 1.6;
        } else {
          newX = -0.15 * x + 0.28 * y;
          newY = 0.26 * x + 0.24 * y + 0.44;
        }

x = newX;
        y = newY;

const pixelX = width / 2 + x * 50; // scaling factor
        const pixelY = height - y * 50; // scaling factor

ctx.fillStyle = 'green';
        ctx.fillRect(pixelX, pixelY, 1, 1);
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      drawBarnsleyFern(100000);
    }

drawFractal();
  </script>
</body>
</html>

Output should look like this:

Things to Try

• Color is always a good starting point - different parts of the fern different colors
• Different number of iterations (gradient - as the iterations increase the color gradually changes)
• Draw multiple ferns on screen (different locations, size and orientation)
• User input - let the user 'click' on screen and add fern at the location they clicked
• Change the direction the fern leaf faces (e.g., instead of to the right, change it so it points to the left)
• Amplify and change the 'angle' - modify how 'curved' the fern leaf is (add a scale factor)
• Modify the iteration loop - algorithm - e.g., trigonometric functions, power, scale, offset
• Randomness - try other random functions (non-linear noise, brown noise, pink noise)

Apollonian Gasket Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>Apollonian Gasket Fractal</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="apollonianGasketCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('apollonianGasketCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawApollonianGasket(x, y, radius, depth) {
      if (depth === 0) {
        return;
      }

// Draw the current circle
      ctx.beginPath();
      ctx.arc(x, y, radius, 0, 2 * Math.PI);
      ctx.strokeStyle = 'white';
      ctx.stroke();

// Calculate the radii of the three new circles
      const r1 = radius / 2;
      const r2 = radius / 2;
      const r3 = radius / 3;

// Recursively draw the three new circles
      drawApollonianGasket(x + radius - r1, y, r1, depth - 1);
      drawApollonianGasket(x - radius + r2, y, r2, depth - 1);
      drawApollonianGasket(x, y + radius - r3, r3, depth - 1);
      drawApollonianGasket(x, y - radius + r3, r3, depth - 1);
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const centerX = width / 2;
      const centerY = height / 2;
      const initialRadius = 200;
      const initialDepth = 4;

drawApollonianGasket(centerX, centerY, initialRadius, initialDepth);
    }

drawFractal();
  </script>
</body>
</html>

Output should look like this:

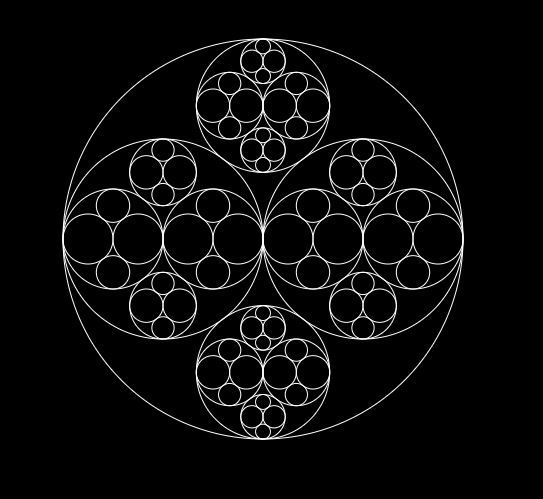
Things to Try

• Making the different circles different colors (fill) - e.g., as the recursion depth increases and the circles get smaller, draw them in a different color
• Try drawing a shape inside the circle (e.g., a triangle, hexagon, pentagon - that matches the diameter of the circle)
• Instead of drawing circles draw hexagons

Menger Sponge Fractal

Click for details

Essentially you just split the square into 9 pieces and remove the middle. You then repeat with the children (not the one you removed the middle from).

<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>2D Menger Sponge Fractal</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #fff;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="mengerSpongeCanvas" width="800" height="800"></canvas>
  <script>
    const canvas = document.getElementById('mengerSpongeCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawMengerSponge(x, y, size, depth) {
      if (depth === 0) {
        ctx.fillRect(x, y, size*0.9, size*0.9);
      } else {
        const newSize = size / 3;

// Draw the central square in some special way?
        //drawMengerSponge(x + newSize, y + newSize, newSize, depth - 1);

// Draw the surrounding eight squares
        for (let i = 0; i < 3; i++) {
          for (let j = 0; j < 3; j++) {

if ( (i == 1 && j == 1) ) {
                continue;
            }

drawMengerSponge(x + i * newSize, y + j * newSize, newSize, depth - 1);
          }
        }
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const initialSize = 400;
      const initialDepth = 3;

drawMengerSponge(width / 2 - initialSize / 2, height / 2 - initialSize / 2, initialSize, initialDepth);
    }

drawFractal();
  </script>
</body>
</html>

Output should look like this:

Things to Try

• Color - try changing the color - so for each depth the drawn squares are drawn a different color
• Draw a pattern inside each square
• Rotate each square as it increases in depth
• Random - add some randomness to each square as they're draw/depth progresses (only a small amount)
• Instead of squares draw other shapes - hexigon, pentigon, ...
• Try other dimensions - instead of 3x3 - try 5x5, 7x7...
• Other shapes - instead of dividing into squares - split into circles or hexagons

Cantor Set (2D Lines)

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>2D Cantor Set Fractal</title>
  <style>
    body {
      min-height: 600px;
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #fff;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="cantorSetCanvas" width="800" height="200"></canvas>
  <script>
    const canvas = document.getElementById('cantorSetCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawCantorSet(x, y, length, depth) {
      if (depth === 0) {
        ctx.fillRect(x, y, length, 5); // Change the second parameter to adjust the height of the line
      } else {
        const newLength = length / 3;

// Draw the central line
        ctx.fillRect(x + newLength, y, newLength, 5); // Change the second parameter to adjust the height of the line

// Recursively draw the two smaller segments
        drawCantorSet(x, y + 25, newLength, depth - 1);
        drawCantorSet(x + 2 * newLength, y + 25, newLength, depth - 1);
      }
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const initialLength = 800;
      const initialDepth = 3;

drawCantorSet(0, height / 2 - 5, initialLength, initialDepth);
    }

drawFractal();
  </script>
</body>
</html>

Output looks like this:

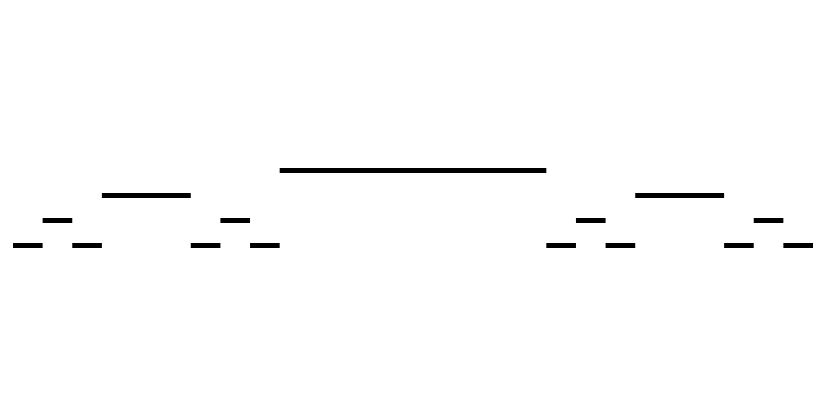
Things to Try

• Make the different lines different colors (based it on the depth)
• Instead of lines draw a shape (using the length and position of the line as the dimension and centre of the shape - shapes, such as circles, cubes, hexagons, ..)

Pythagorean Tree Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>2D Pythagorean Tree Fractal</title>
  <style>
    body {
      margin: 0;
      display: flex;
      justify-content: center;
      align-items: center;
      height: 100vh;
      background-color: #000;
    }
    canvas {
      border: 1px solid #fff;
    }
  </style>
</head>
<body>
  <canvas id="pythagoreanTreeCanvas" width="800" height="600"></canvas>
  <script>
    const canvas = document.getElementById('pythagoreanTreeCanvas');
    const ctx = canvas.getContext('2d');
    const width = canvas.width;
    const height = canvas.height;

function drawPythagoreanTree(x, y, length, angle, depth) {
      if (depth === 0) {
        return;
      }

const x1 = x;
      const y1 = y;
      const x2 = x1 + length * Math.cos(angle);
      const y2 = y1 + length * Math.sin(angle);

ctx.beginPath();
      ctx.moveTo(x1, y1);
      ctx.lineTo(x2, y2);
      ctx.strokeStyle = 'white';
      ctx.stroke();

const newLength1 = length * 0.7;
      const newLength2 = length * 0.5;

const newAngle1 = angle - Math.PI / 4;
      const newAngle2 = angle + Math.PI / 4;

drawPythagoreanTree(x2, y2, newLength1, newAngle1, depth - 1);
      drawPythagoreanTree(x2, y2, newLength2, newAngle2, depth - 1);
    }

function clearCanvas() {
      ctx.clearRect(0, 0, width, height);
    }

function drawFractal() {
      clearCanvas();
      const initialLength = 200;
      const initialAngle = -Math.PI / 2; // pointing upwards
      const initialDepth = 7;

drawPythagoreanTree(width / 2, height, initialLength, initialAngle, initialDepth);
    }

drawFractal();
  </script>
</body>
</html>

The output should look like this:

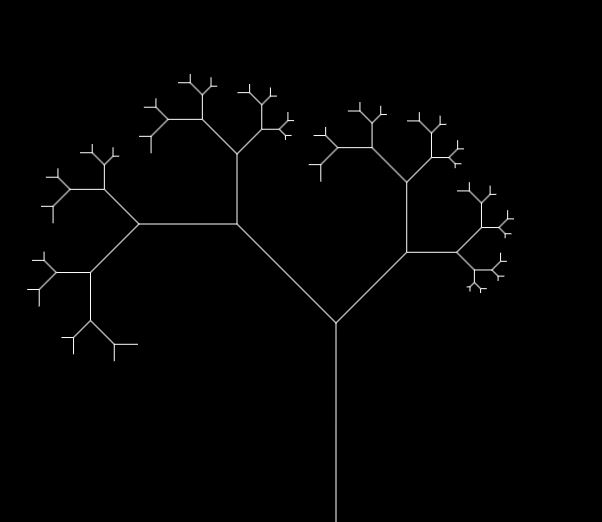
Things to Try

• Add color - as the depth increases so does the color - changes from brown to green (e.g., trunk is brown while very end branches are 'green' representing the leaves)
• Increasing the depth
• Randomness - explore adding in small amounts of randomness into the recursive function (e.g., randomly subtracting different depths instead of just 1, slight deviations in angle and length)
• Moving the tree around (offset position)
• Draw multiple trees on screen (e.g., forest of trees - different sizes, position, with randomness so they're all unique)

Tetrahex Fractal

Click for details

<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>Tetrahex Fractal</title>
  <style>
    body { margin: 0; }
    canvas { display: block; }
  </style>
</head>
<body>
  <canvas id="fractalCanvas" width='500' height='500'></canvas>
  <script>
    // WebGL setup
    const canvas = document.getElementById('fractalCanvas');
    const gl = canvas.getContext('webgl');

if (!gl) {
      console.error('Unable to initialize WebGL. Your browser may not support it.');
    }

// Vertex and fragment shaders
    const vertexShaderSource = `
      attribute vec4 a_position;
      void main() {
        gl_Position = a_position;
      }
    `;

const fragmentShaderSource = `
      precision mediump float;
      void main() {
        gl_FragColor = vec4(1.0, 1.0, 1.0, 1.0);
      }
    `;

// Compile shaders
    function compileShader(gl, source, type) {
      const shader = gl.createShader(type);
      gl.shaderSource(shader, source);
      gl.compileShader(shader);

if (!gl.getShaderParameter(shader, gl.COMPILE_STATUS)) {
        console.error('Shader compilation error:', gl.getShaderInfoLog(shader));
        gl.deleteShader(shader);
        return null;
      }

return shader;
    }

const vertexShader = compileShader(gl, vertexShaderSource, gl.VERTEX_SHADER);
    const fragmentShader = compileShader(gl, fragmentShaderSource, gl.FRAGMENT_SHADER);

// Create shader program
    const shaderProgram = gl.createProgram();
    gl.attachShader(shaderProgram, vertexShader);
    gl.attachShader(shaderProgram, fragmentShader);
    gl.linkProgram(shaderProgram);
    gl.useProgram(shaderProgram);

// Set up vertices for Tetrahex fractal
    const vertices = [];

function generateTetrahex(vertices, depth, a, b, c) {
      if (depth === 0) {
        vertices.push(a[0], a[1], b[0], b[1], c[0], c[1]);
      } else {
        const ab = [(a[0] + b[0]) / 2, (a[1] + b[1]) / 2];
        const ac = [(a[0] + c[0]) / 2, (a[1] + c[1]) / 2];
        const bc = [(b[0] + c[0]) / 2, (b[1] + c[1]) / 2];

const mid = [(ab[0] + ac[0] + bc[0]) / 3, (ab[1] + ac[1] + bc[1]) / 3];

generateTetrahex(vertices, depth - 1, a, ab, mid);
        generateTetrahex(vertices, depth - 1, b, bc, mid);
        generateTetrahex(vertices, depth - 1, c, ac, mid);
        generateTetrahex(vertices, depth - 1, ab, bc, ac);
      }
    }

generateTetrahex(vertices, 6, [-1, -1], [1, -1], [0, 1]);

// Create buffer and bind vertices
    const vertexBuffer = gl.createBuffer();
    gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
    gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);

const positionAttribLocation = gl.getAttribLocation(shaderProgram, 'a_position');
    gl.vertexAttribPointer(positionAttribLocation, 2, gl.FLOAT, false, 0, 0);
    gl.enableVertexAttribArray(positionAttribLocation);

// Render loop
    function render() {
      gl.clearColor(0.0, 0.0, 0.0, 1.0);
      gl.clear(gl.COLOR_BUFFER_BIT);
      
      gl.drawArrays(gl.TRIANGLES, 0, vertices.length / 2);

requestAnimationFrame(render);
    }

render();
  </script>
</body>
</html>

The output looks like this:

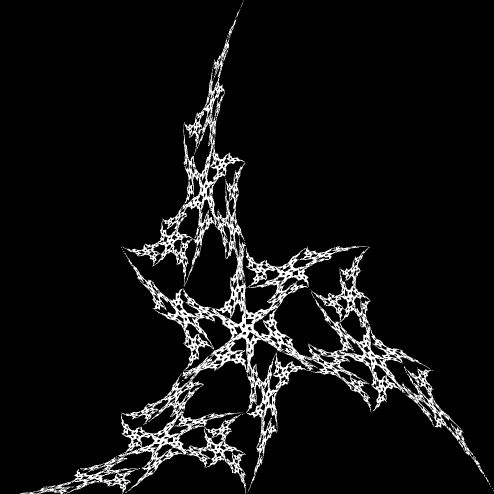
Things to Try

• Change the colors (as it recurses to add extra detail, change the colors)
• Try different resolutions (e.g., 2, 5, 10, ...)

Burning Ship Fractal Javascript

Click for details

<html>
<head>
    <title>xbdev.net Burning Ship Fractal</title>
    <style>
        body {
            margin: 0;
            overflow: hidden;
            min-height:600px;
        }
        canvas {
            display: block;
        }
    </style>
</head>
<body>
    <canvas id="canvas" width='600' height='600'></canvas>
    <script>
        // Define canvas and context
        const canvas = document.getElementById('canvas');
        const ctx = canvas.getContext('2d');

// Set canvas size
        const width = canvas.width = window.innerWidth;
        const height = canvas.height = window.innerHeight;

// Define constants for the fractal
        const maxIterations = 100;
        const zoom = 150;
        const offsetX = -2;
        const offsetY = -1.5;
        const escapeRadius = 2;

// Function to calculate burning ship fractal
        function burningShip(x0, y0) {
            let x = 0;
            let y = 0;
            let i = 0;

while (x * x + y * y < escapeRadius * escapeRadius && i < maxIterations) {
                let xTemp = x * x - y * y + x0;
                y = Math.abs(2 * x * y) + y0;
                x = xTemp;
                i++;
            }

if (i === maxIterations) {
                return 0;
            } else {
                return i / maxIterations * 255;
            }
        }

// Render the fractal
        function render() {
            for (let x = 0; x < width; x++) {
                for (let y = 0; y < height; y++) {
                    const zx = (x / zoom) + offsetX;
                    const zy = (y / zoom) + offsetY;
                    const color = burningShip(zx, zy);
                    ctx.fillStyle = `rgb(${color}, ${color}, ${color})`;
                    ctx.fillRect(x, y, 1, 1);
                }
            }
        }

// Render the fractal when the page loads
        window.onload = function() {
            render();
        };
    </script>
</body>
</html>

The output looks like this:

Thigns to Try

• Adding colors (emphasis edges, centre, ..)
• Try different levels of detail
• Draw the ship at different x,y locations, size and orientation
• Draw multiple ships on screen at different locations and sizes
• Adding some randomness to the result (small random values)
• Mix in some trignometric functions (add some rythmic character)

Kaleidoscope Fractal

Click for details

<html>
<head>
    <title>xbdev.net Kaleidoscope Fractal</title>
    <style>
        canvas {
            border: 1px solid black;
        }
    </style>
</head>
<body>
    <canvas id="kaleidoscopeCanvas" width="600" height="600"></canvas>

function drawFractal(x, y, size, depth) {
            if (depth === 0) return;
            ctx.beginPath();
            ctx.arc(x, y, size, 0, 2 * Math.PI);
            ctx.stroke();

for (let i = 0; i < numSlices; i++) {
                const angle = i * sliceAngle;
                const newX = x + size * Math.cos(angle);
                const newY = y + size * Math.sin(angle);
                drawFractal(newX, newY, size / 2, depth - 1);
            }
        }

function drawKaleidoscopeFractal() {
            ctx.clearRect(0, 0, canvas.width, canvas.height);
            drawFractal(centerX, centerY, 200, depth);
        }

drawKaleidoscopeFractal();
    </script>
</body>
</html>

The output looks like this:

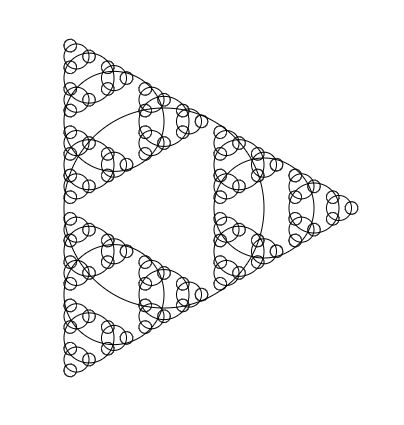
Thigns to Try

• Change the sliceAngles and the depth parameters (see the different fractal shapes/level of detail)
• Try with other shapes instead of circles (e.g., squares, triangles, hexagons, ...)
• Instead of flat black and white shapes, try and insert 'images' - repeats the image in a pattern
• Add colors - each depth uses a different color
• Explore animating the effect so it transitions and rotates

Advert (Support Website)

Visitor: